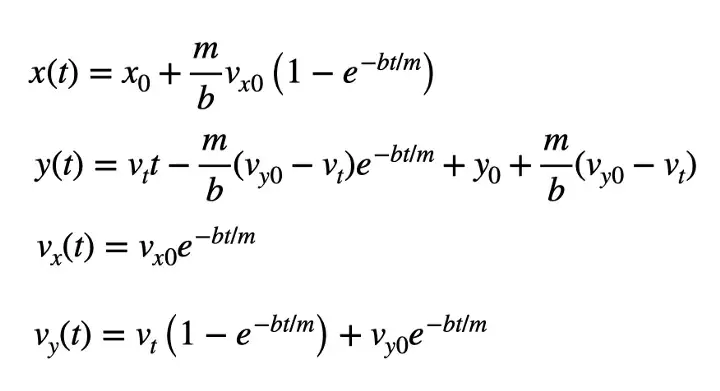petrak@'s mods forum

Posted: **Sat Dec 24, 2022 6:26 am**

This is a hex that's able to launch an item or falling block to hit any target of your choice within at least 1000 blocks, assuming the intermediate chunks are loaded. It's the same concept as my Precision Launcher hex, but with a totally different (and simpler and shorter and faster) implementation. This hex uses Hexal's macro feature in a couple places; the macros are listed below the main hex. (You can also skip using macros and directly draw the patterns if you want — they're pretty short. The hex also uses Hexal for some math stuff though, so you need it anyway.)

Video demo

Item Cannon
This hex is meant to be used with a CAD. Sneak-click to set the target block, then click items or falling blocks to launch them to the target.
It should work for other entity types with some modification, though I haven't tested it. Constants are written in several places in the hex, all commented. To use this hex with entities other than items or falling blocks, replace the constants with the corresponding values for your desired entity type from this table.

Code: Select all

{
    Mind's Reflection
    Stadiometer's Purification
    Numerical Reflection: 1.5
    Maximus Distillation
    Consideration: {
        // get target entity and distances to target block

        {
            Bookkeeper's Gambit: - // target block placeholder
        }
        Flock's Disintegration

        Mind's Reflection
        Compass' Purification
        Mind's Reflection
        Alidade's Purification
        Scout's Distillation

        Undertaker's Gambit
        Compass' Purification II
        Subtractive Distillation
        
        Vector Disintegration
        Rotation Gambit
        Numerical Reflection: 0
        Rotation Gambit
        Vector Exaltation
        
        Gemini Decomposition
        Length Purification
        Undertaker's Gambit
        Division Distillation
        Rotation Gambit II
        Jester's Gambit

        // algorithm to get launch parameters

        Prospector's Gambit
        Numerical Reflection: 50 // 1/drag
        Division Distillation
        Numerical Reflection: 8 // tune as necessary; should be >> v_terminal
        Minimization Distillation
        
        Prospector's Gambit
        Numerical Reflection: 35 // tune as necessary
        Division Distillation
        Numerical Reflection: 0
        Maximization Distillation
        
        Additive Distillation
        Numerical Reflection: 2 // v_terminal
        Additive Distillation
        
        Undertaker's Gambit
        Numerical Reflection: 2 // v_terminal
        Additive Distillation

        Rotation Gambit II
        Dioscuri Gambit

        Numerical Reflection: 0
        Minimus Distillation
        Numerical Reflection: 50 // 2/gravity
        Numerical Reflection: 25 // 1/gravity
        Augur's Exaltation
        
        Multiplicative Distillation
        Numerical Reflection: 0
        Numerical Reflection: 2
        Flock's Gambit
        Huginn's Gambit
        
        Rotation Gambit
        Numerical Reflection: 10 // Newton's Method max iterations
        Gemini's Gambit
        Numerical Reflection: 10 // as above
        Flock's Gambit
        
        Consideration: {
            Euler's Reflection
            Muninn's Reflection
            Flock's Disintegration
            Bookkeeper's Gambit: v
            
            Undertaker's Gambit
            Numerical Reflection: -50 // -1/drag
            Division Distillation
            Power Distillation
            
            Rotation Gambit
            Prospector's Gambit
            Dioscuri Gambit
            
            Numerical Reflection: 1
            Subtractive Distillation
            Multiplicative Distillation
            Numerical Reflection: 50 // 1/drag
            Multiplicative Distillation
            
            Rotation Gambit II
            Multiplicative Distillation
            Numerical Reflection: 2 // v_terminal
            Subtractive Distillation
            Jester's Gambit
            
            Numerical Reflection: 3 // should be 4, but Fisherman II is broken right now
            Fisherman's Gambit II
            Numerical Reflection: 2 // v_terminal
            Multiplicative Distillation
            Additive Distillation
            
            Numerical Reflection: 5
            Fisherman's Gambit
            Additive Distillation
            
            Gemini Decomposition
            Length Purification
            
            // Newton's Method epsilon
            Numerical Reflection: 1
            Numerical Reflection: 10
            Numerical Reflection: 100
            Multiplicative Distillation
            Division Distillation
            Minimus Distillation

            {
                Charon's Gambit
                Bookkeeper's Gambit: -
            }
            Flock's Disintegration
            Augur's Exaltation
            Hermes' Gambit

            Jester's Gambit
            Division Distillation
            Rotation Gambit
            Additive Distillation
            
            Jester's Gambit
            Numerical Reflection: 2
            Flock's Gambit
            Huginn's Gambit
        Consideration: }

        Jester's Gambit
        Thoth's Gambit
        Bookkeeper's Gambit: vv

        Muninn's Reflection
        Numerical Reflection: 1
        Selection Distillation
        
        Numerical Reflection: 1
        Jester's Gambit

        Numerical Reflection: 4
        Gemini's Gambit
        Numerical Reflection: 5
        Flock's Gambit
        
        Running Product Purification
        Running Sum Purification
        Retrograde Purification
        Numerical Reflection: 0
        Selection Distillation
        
        Rotation Gambit
        Multiplicative Distillation
        Numerical Reflection: 50 // 1/drag
        Division Distillation
        
        // launch the item
        
        Rotation Gambit
        Multiplicative Distillation
        Vector Disintegration
        Bookkeeper's Gambit: v-
        
        Rotation Gambit
        Jester's Gambit
        Vector Exaltation
        
        Prospector's Gambit
        Gemini Decomposition
        Pace Purification

        // don't subtract velocity for items
        // because pace returns the item's FLOATING SPEED when it's NOT MOVING
        Jester's Gambit
        Compass' Purification
        Entity Purification: Item
        Augur's Purification
        {
            Bookkeeper's Gambit: v
            Subtractive Distillation
        }
        Flock's Disintegration
        Augur's Exaltation
        Hermes' Gambit
        
        Impulse
    Consideration: }
    Consideration: {
        // set the target block
        
        Scribe's Reflection
        Numerical Reflection: 6
        
        Mind's Reflection
        Compass' Purification
        Mind's Reflection
        Alidade's Purification
        
        Dioscuri Gambit
        Archer's Distillation
        Rotation Gambit II
        Architect's Distillation
        
        // aim for the very top of the target block, not half a block above it
        Numerical Reflection: 2
        Division Distillation
        Additive Distillation
        
        Surgeon's Exaltation
        Scribe's Gambit
    Consideration: }
    Augur's Exaltation
    Hermes' Gambit
}

Minimization Distillation
num, num -> num

Min function.

Code: Select all

{
    Dioscuri Gambit
    Minimus Distillation
    Rotation Gambit II
    Augur's Exaltation
}

Maximization Distillation
num, num -> num

Max function.

Code: Select all

{
    Dioscuri Gambit
    Maximus Distillation
    Rotation Gambit II
    Augur's Exaltation
}

Posted: **Sat Dec 24, 2022 7:11 am**

How It Works
In this post, I'll explain how the Item Cannon works and how I arrived at this solution.
CW: math

This hex's goal is to find an initial velocity to launch an item in order to make it travel a given distance. In other words, given a horizontal and vertical distance, find a horizontal and vertical initial velocity that makes the projectile travel that distance. Basically, this is a 2D projectile motion problem with linear drag, since that's the type of air resistance used in Minecraft.

I started with equation (186) [1], which can be rearranged to give an initial guess for the horizontal velocity: v_0x = g*x_dist/v_term = drag*x_dist
This formula holds as long as v_0y >> v_term, so we can pick some initial v_0y that follows that constraint. After some trial and error, I arrived at this formula: v_0y = max(y_dist/35, 0) + min(x_dist/drag, 8) + v_t

Unfortunately, it's not quite that simple. To see why, we'll need to take a look at the equations of motion for linear drag [2]:

The graph below is what those equations look like, plotted with the above formulas and some chosen x_dist and y_dist. Green is y(t), purple is x(t). The horizontal axis is time, and the vertical axis is distance. (I've flipped both functions over the horizontal axis to make it easier to understand.) [3]

Notice how x(t) is somewhere above zero at the second root of y(t). That's a problem, because it means we'll miss the target by a few blocks. Let's zoom in a bit more.

See that gap between x(t) and y(t) at the root? Let's take that number (5.368 in this case), add it to our x_dist value in the v_0x formula, and plot it again.

The gap got smaller! Do that a few more times, and you end up with a *very* precise estimate for the initial x velocity.

One more problem: how do we find the second root of y(t)? Unfortunately, as far as I can tell, there doesn't seem to be an analytical solution. However, this function is pretty well-behaved, so we can just use Newton's Method, using the flight time equations (190) or (191) [1] (depending on initial conditions) as starting guesses.

So that's basically how this algorithm works. My Python implementation is below if you're curious. There's probably a better way to solve this problem, but this is already far more practical than my previous solution, so I'm happy with it.

Python Implementation

Code: Select all

import math
from typing import Callable


def newton(f: Callable[[float], float], x0: float, df: Callable[[float], float], epsilon: float, iterations: int):
    x = x0
    for _ in range(iterations):
        y = f(x)
        if abs(y) < epsilon:
            return x

        dy = df(x)
        if dy == 0:
            return None

        x -= y/dy
    return None


# items
D = -0.02
D_inv = -50
g = 0.04
g_inv = 25
v_t = 2
v_0y_factor = 35

# ender pearls (untested)
# D = 0.01
# D_inv = 100
# g = 0.03
# g_inv = 100/3
# v_t = 3
# v_0y_factor = 70


# generic function
def get_launch_params(dx: float, dy: float) -> tuple[float, float] | None:
    v_0y = max(dy/v_0y_factor, 0) + min(dx*-D, 8) + v_t

    f = lambda t: v_t*t + dy - ((v_0y + v_t) / D)*(math.exp(D*t) - 1)
    df = lambda t: v_t - (v_0y + v_t)*math.exp(D*t)

    t0 = v_0y/g
    if dy < 0:
        t0 *= 2

    t1 = newton(f, t0, df, 1/1000, 10)
    if t1 is None:
        return None

    v_0x = 0
    delta = 0
    for _ in range(5):
        v_0x = g*(dx + delta)/v_t
        x1 = -v_0x*(1 - math.exp(D*t1))/D - dx
        delta -= x1
    
    return v_0x, v_0y


# refactored with all variables inlined and a lot of simplification
# this was my reference when writing the Hex version
def get_launch_params_hex(x_dist: float, y_dist: float) -> tuple[float, float]:
    # const
    v_0y = max(y_dist/35, 0) + min(x_dist/50, 8) + 2
    B = v_0y + 2
    
    # var
    t1 = v_0y * (50 if y_dist < 0 else 25)
    A = 0

    for _ in range(10):
        A = math.exp(t1/-50)
        y = y_dist + 2*t1 + B*50*(A - 1)
        if abs(y) < 1/1000:
            break

        t1 += y/(A*B - 2)
    return x_dist*(A**4 + A**3 + A**2 + A + 1)/50, v_0y

Sources
[1] https://farside.ph.utexas.edu/teaching/ ... ode29.html
[2] https://rjallain.medium.com/projectile- ... 489b8045d7
[3] https://www.desmos.com/calculator/bnieeqxtik

petrak@'s mods forum

Item Cannon

Item Cannon

Re: Item Cannon